みなさんこんにちは。マネージドサービス部MSS課の塩野(正)です。 今回はAmazon CloudWatch AlarmやNew Relicなどの監視システムで導入されているAnomary Detection(異常検知)についての深堀りをした記事です。
異常検知というとなんだか便利そうな機能だなぁ・・というイメージが先走ってしまいますが、使い方を間違えるとノイズを減らす便利な機能がノイズまみれになる可能性があるということで、アノマリー検知の付き合い方を考えていこうというお話になります。
目次
Anomary Detectionとは
Anomary Detectionは異常検知と表現されることが多く、異常検知の状態とはいつもと違う状態のことを指します。この「いつもと様子が違う」というのは、どうやって判断すればいいのでしょうか。例えば、普段は30分で終わるバッチ処理が、今日は1時間かかったとします。これは明らかに「異常」ですよね。単純に「CPU使用率が80%以上」を異常とするのではなく、「いつもと比べて明らかにおかしい」状態を検知するのが、Anomaly Detectionの基本的な考え方です。
New Relic監視としてのAnomary Detectionの定義
Anomaly監視の定義
New RelicのAnomaly監視の定義を公式ドキュメントから紐解きましょう。
異常感度しきい値を設定する 異常検出は、以前のアクティビティに基づいて次のデータ ポイントがどうなるかを予測します。異常検出のしきい値は、実際の値が予測値からどれだけ離れているかを許容するアラート条件の感度を制御します。しきい値は、信号値が予測値からどれだけ離れているかを示す標準偏差の数です。過去 7 日間のデータの予測値と実際の値の間の標準偏差を追跡します。
少なくとも公式ドキュメントを見る限りでは、New RelicのAnomaly detectionでは独自の標準偏差を使用した異常検知が行われていることが推測されます。
New RelicのAnomary監視の実際
では、New RelicのAnomary監視でどのような設定ができるか見てみましょう。一般的に標準偏差という言葉を思い浮かべると、標準偏差自体はデータのばらつきを示す「指標」であるものの、そのデータが正規分布のどこにあるのかを想像するケースが多いのではないかと推測しています。正規分布における標準偏差の意味として、平均値±1標準偏差の範囲に、全体の約68%のデータが含まれ、平均値±2標準偏差の範囲に、全体の約95%のデータが含まれ、平均値±3標準偏差の範囲に、全体の約99.7%のデータが含まれるというアレです。
実際の設定がどうなっているか確認してみましょう。
- デフォルトの閾値:3σ
- 閾値の最大値:1000σ
閾値の値を見る限り、なんだかおかしなことになっていますね(笑)でも、これはこれで正しい仕様になります。なぜこのようなことになっているかというのを深堀りするためには、標準偏差というものをもっと理解する必要があるため、ここから少しだけ教科書的なお話をしたいと思います。
移動平均と標準偏差
移動平均とは
私たちが標準的な監視で使っている閾値監視は、それぞれのデータポイントを評価時間で集計した移動平均線になります。実は移動平均線自体にもいくつか考え方があるのですが、ここでは一般的に使われていると考えられている単純移動平均(SMA)に言及して話を進めたいと思います。
移動平均の計算
単純移動平均(SMA)とは、指定した期間(ウィンドウ)のデータの平均値を計算し、それを順次ずらしていく方法です。例えば5分間のCPU使用率データが下記だった場合で指定した期間が3分間だった場合の計算例を見てみましょう。
# 例)CPU 使用率データ 1分目: 50% 2分目: 60% 3分目: 40% 4分目: 70% 5分目: 55% 6分目: 65% 7分目: 45%
最初の1点目の計算は下記の通りになります。
# 最初の3点(1-3分目)の計算 (50 + 60 + 40) ÷ 3 = 50%
次の2点目の計算は下記の通りになります。
# 次の3点(2-4分目)の計算 (60 + 40 + 70) ÷ 3 = 56.7%
その次の3点目の計算は下記の通りになります。
# その次の3点(3-5分目)の計算 (40 + 70 + 55) ÷ 3 = 55%
このように、決められたデータポイントのウインドウをずらしながら計算していくのが、単純移動平均を使った一般的な監視になります。単純移動平均を使った場合のメリットデメリットとして、以下のような点が考えられます。
- メリット
- 計算が簡単
- 理解しやすい
- ノイズを減らせる
- デメリット
- ウインドウサイズを小さくすると、ノイズが多くなる
- ウインドウサイズを大きくすると、急激な変化への反応が遅い
- すべてのデータに同じ重みを付けるため、新しいデータの影響が分かりにくい
標準偏差
標準偏差とは
標準偏差とはデータのばらつき具合を数値で表したもので、「平均値からどれくらい離れているか」を示します。その平均値を中心に左右対称となっている確率分布で示したものが、下記のような正規分布図となり、両者の関係性は以下の通りです。
- 正規分布における標準偏差の意味
- 平均値±1標準偏差の範囲に、全体の約68%のデータが含まれる
- 平均値±2標準偏差の範囲に、全体の約95%のデータが含まれる
- 平均値±3標準偏差の範囲に、全体の約99.7%のデータが含まれる

ここまでは一般的なお話になりますが、閾値の最大値が1000σになっている理由について、ここから少し踏み込んで話をしていきましょう。
標準偏差と時系列データ
割と知っている人は知っているのですが、この標準偏差の閾値設定が変なのは時系列データだからというのが答えになります。例えば、下記のホームページに以下のような記載があります。監視データの殆どは時系列データになるため、「各観測値は独立であるという通常の統計解析における仮定が成立しない」ため「時間軸上の構造的あるいは周期的変動を考慮した特有な分析手法が必要」になります。
時系列データは,通常,時間軸上で等間隔に観測される系列的なデータ群をいう.そのため,各観測値は独立であるという通常の統計解析における仮定が成立しないので,これらの時間軸上の構造的あるいは周期的変動を考慮した特有な分析手法が必要になる (株)日科技研:新手法例 時系列分析(ARIMAモデル)の機能とその活用(株式会社日本科学技術研修所 王 克義)|導入事例
もう少しわかりやすい例で見てみましょう。下記は為替チャートに標準偏差のインジケーターである「ボリンジャーバンド」を2σの設定で追加した画像になりますが、パッと見た感じバンドが大きくなったり小さくなったりしているのが分かるかと思います。時系列データのため、価格変動が小さいほどバンド幅が小さくなり、価格変動が大きくなればバンド幅が大きくなるような風に見えていますが、実際そのような挙動になります。
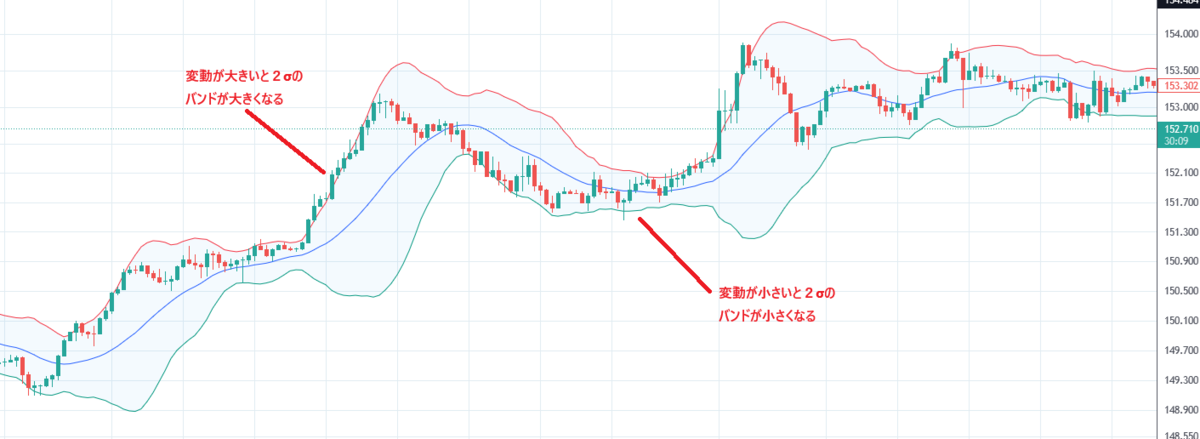
では、バンド幅を広げてみるとどのように見えるのでしょうか。下記は10σの設定にした画像になりますが、変動が大きい所は極端に大きなバンド幅になっていることが見て取れます。実際の監視システムではここまで極端なバンド幅を描くことは少ないものの、このようなクセがあることは少なくとも理解できたのではないかと思います。

まとめると、メトリクスの変動が極端に小さいシステムの場合、バンド幅の設定次第ではノイズアラートが多数発生する傾向にあり、メトリクスの変動がある程度のシステムだと、逆に大きくしすぎると異常値が出ても検知できなくなる恐れがあったりします。また、2σの画像を見ると、一部の箇所において価格がバンド幅に沿って推移しているような状況があったりします。実際の監視システムであれば、緩やかなメトリクスの上昇がこのケースにあたり、このケースもまた、メトリクスの推移にバンド幅が追従してしまいアラートが発生しない可能性があるという状況になります。
- 大きすぎる標準偏差の問題
- 異常値の検出が難しくなる
- 正常な変動と異常な変動の区別が困難
- アラートの誤検知が増加する可能性がある
- 小さすぎる標準偏差の問題
- ノイズの影響を受けやすくなる
- わずかな変動でもアラートが発生
標準偏差の計算
それでは標準偏差の計算について、具体例を使って分かりやすく説明していきましょう。標準偏差はデータのばらつき具合を数値で表し、「平均値からどれくらい離れているか」を示したものでしたね。それではあるサーバーの5分間のCPU使用率データを使って計算していきます。
# 例)CPU 使用率データ 1分目: 50% 2分目: 60% 3分目: 40% 4分目: 70% 5分目: 55%
まず、CPU使用率データの平均値を算出します。
平均 = (50 + 60 + 40 + 70 + 55) ÷ 5 = 55%
次に、各データと平均との差を計算します。
1分目の差: 50 - 55 = -5 2分目の差: 60 - 55 = 5 3分目の差: 40 - 55 = -15 4分目の差: 70 - 55 = 15 5分目の差: 55 - 55 = 0
次に、それぞれの差を2乗にします。
1分目: (-5)² = 25 2分目: (5)² = 25 3分目: (-15)² = 225 4分目: (15)² = 225 5分目: (0)² = 0
次に、2乗した値の平均(分散)を計算します。
分散 = (25 + 25 + 225 + 225 + 0) ÷ 5 = 100
最後に分散の平方根を計算(標準偏差)します。
標準偏差 = √100 = 10
と、こんな感じで各時間毎に計算をしていくわけですが、こうやって書いていても数学が好きな人でない限りは、うっ・・・っとなります。(私はあまり得意な方ではありません)
一般的な標準偏差の話の中で、実用的な解釈をするなら、
- 標準偏差が小さい → データが平均の周りに集中している
- 標準偏差が大きい → データが平均から広く散らばっている
という特徴があります。
監視システムで標準偏差を利用する場合
監視システムでAnomary detection機能(標準偏差)を使った監視をおこなう場合を考慮して、メリット、デメリットを整理してみましょう。
- メリット
- データのばらつきを定量的に評価できる
- 異常検知の基準として使いやすい
- 単位がデータと同じなので解釈しやすい
- デメリット
- 外れ値の影響を受けやすい
- 時系列データでは時間的な相関を考慮できない
- データが正規分布に従っていない場合は解釈が難しい
監視システムでAnomary detection機能(標準偏差)を使った監視をおこなう場合のポイントとして、データのばらつきを定量的に評価できる反面、時系列データでは時間的な相関を考慮できない ことや、外れ値の影響を受けやすい ことなどから、一般的な正規分布での目安となる3σを超えて変動することがあるため、New Relicなどの監視システムでは閾値が3σ以上の値が用意されていると解釈できます。
もう少し特性をわかりやすく整理してみましょう。
- 標準偏差が小さい
- → 評価時間内におけるCPU使用率などの変動が極めて小さい
- → 余計なアラームが発生しやすい
- → 評価時間内におけるCPU使用率などの変動が極めて小さい
- 標準偏差が大きい
- → 評価時間内におけるCPU使用率などの変動が極めて大きい
- → 閾値にかからず必要なアラームが鳴らない
- → 評価時間内におけるCPU使用率などの変動が極めて大きい
という点をよく理解しておく必要があります。また、単純な変動率だけではなく、システムにおける標準偏差の計算時間(New Relicの場合は7日+その前の7日の14日)も考慮しておく必要があり、例えばスマホゲームのアプリやEコマースなどで月初だけ(月末だけ)イベントをやるような場合、評価期間が14日に収まらないことが容易に想像できます。こういった特性を踏まえて、標準偏差の計算時間の間に変動パターンがいくつかあるようなシステムの場合でAnomary監視を行いたい場合は、特定のイベントなどに合わせて動的に閾値をコントロールするなどの対応を行うほうが、より本来のAnomary監視にあった対応になるということになります。
つまり、監視対象のシステム特性を理解しないままアラーム設定すると、Anomary監視は全く使い物にならないとか、使いにくいものになる可能性があるという点に留意する必要があるということです。
まとめ
実はAnomary監視を取り入れる前からこの特性に薄々気が付いていて、実際試してみたらやっぱりそうだったよね~ということからこの記事を書きました。ものすごく余談な話になりますが、為替や株などの世界で使われている標準偏差を使った監視(インジケーター)はボリンジャーバンドと呼ばれており、標準偏差の軸2σや3σだけではなく%bを使って勢い(変動率)まで見る必要があるよとインジケータの開発者であるジョン・ボリンジャーさんが仰られています。為替にしてもサーバーのCPU使用率にしても、監視データ上は時系列となってしまうため、単純な2σや3σという考え方だけではなくデータの特性までちゃんと考慮しないと本来あるべき姿の監視にはならないよという点を頭の片隅に置いてもらえたら嬉しいです。



